Будьте всегда в курсе!
Узнавайте о скидках и акциях первым
Новости
Все новости
7 марта 2024
С 8 Марта!
Как решать задание 16 ЕГЭ по математике (профиль)
Алгоритм решения задания №16 в профильном ЕГЭ по математике 2024 (экономическая задача)
1. Анализ условия задачи: Тщательно прочитайте текст задачи, чтобы понять экономический контекст и выявить основные переменные и параметры.
2. Формулирование математической модели: Переведите экономические условия в математическую модель, используя уравнения, неравенства или функции. Обычно это включает определение функции дохода, расхода или прибыли.
3. Использование математических инструментов: Примените подходящие математические методы для решения задачи, например, дифференцирование для нахождения экстремумов функции, решение уравнений или систем уравнений.
4. Анализ критических точек: Если требуется определить максимальную или минимальную прибыль, найдите критические точки функции (где производная равна нулю или не существует) и определите их характер.
5. Учёт ограничений задачи: Убедитесь, что решение удовлетворяет всем ограничениям задачи, таким как неотрицательность переменных или заданные диапазоны значений.
6. Проверка и анализ ответа: Перепроверьте решение, особенно арифметические и алгебраические вычисления, и убедитесь, что ответ логичен в контексте задачи.
7. Формулировка ответа: Запишите ответ в требуемом формате, убедившись, что он полный и соответствует заданным условиям.
За каждым заданием второй части профильного ЕГЭ по математике уже давно закрепилось неофициальное название: так, задание 16 учителя и учащиеся называют экономической задачей. Это название объединяет задачи на кредиты и вклады, а также задачи на оптимизацию.
Эксперт, который проверяет выполненное Вами задание, выставляет баллы в строгом соответствии с критериями, приведёнными в таблице:
2. Формулирование математической модели: Переведите экономические условия в математическую модель, используя уравнения, неравенства или функции. Обычно это включает определение функции дохода, расхода или прибыли.
3. Использование математических инструментов: Примените подходящие математические методы для решения задачи, например, дифференцирование для нахождения экстремумов функции, решение уравнений или систем уравнений.
4. Анализ критических точек: Если требуется определить максимальную или минимальную прибыль, найдите критические точки функции (где производная равна нулю или не существует) и определите их характер.
5. Учёт ограничений задачи: Убедитесь, что решение удовлетворяет всем ограничениям задачи, таким как неотрицательность переменных или заданные диапазоны значений.
6. Проверка и анализ ответа: Перепроверьте решение, особенно арифметические и алгебраические вычисления, и убедитесь, что ответ логичен в контексте задачи.
7. Формулировка ответа: Запишите ответ в требуемом формате, убедившись, что он полный и соответствует заданным условиям.
За каждым заданием второй части профильного ЕГЭ по математике уже давно закрепилось неофициальное название: так, задание 16 учителя и учащиеся называют экономической задачей. Это название объединяет задачи на кредиты и вклады, а также задачи на оптимизацию.
Эксперт, который проверяет выполненное Вами задание, выставляет баллы в строгом соответствии с критериями, приведёнными в таблице:
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Вы, конечно, заметили, что в критериях нет ни слова о способах решения задания, зато подчёркивается, что нужно обосновать решение?
- Оценивается
математическая грамотность, обоснованность и полнота приведённого решения и ответа, а также отсутствие или наличие вычислительных ошибок
- Не оценивается выбранный Вами способ решения и форма записи.
Что требуется для успешного решения задания 16?
- Понимание всех встречающихся в условии терминов (вклад, кредит, начисление процентов, долг и т. п.)
- Повторить темы
- Проценты,
- Арифметическая и геометрическая прогрессии,
- Наибольшее и наименьшее значение функции.
Кредит банка – сумма денежных средств, которую заёмщик обязуется вернуть банку в соответствии с условиями заключённого договора (проценты, сроки промежуточных платежей и др.). Платёж по кредиту состоит из основного долга и процентов. Основной долг — это размер кредита. А проценты — это сумма, которую берет банк за пользование кредитом.
|
Две схемы решения задач на кредиты |
|
|
Кредит выплачивается равными платежами (аннуитетные платежи), ИЛИ Известными платежами |
Выплаты подбираются так, что сумма долга уменьшается равномерно (дифференцированные платежи) ИЛИ Известно, как меняется сумма долга |
Банковский вклад (или банковский депозит) — сумма денег, переданная лицом банку с целью получить доход в виде процентов, образующихся в ходе финансовых операций с вкладом. Начисление процентов происходит в соответствии с заключённым договором. Если в договоре по вкладу указан доход 5 % годовых, а вклад составляет S рулей, то это значит, что через год на вкладе будет 1,05S рублей.
Ниже приведены примеры решения задания 16 по математике: на кредиты, на вклады и на оптимизацию.
Пример 1.
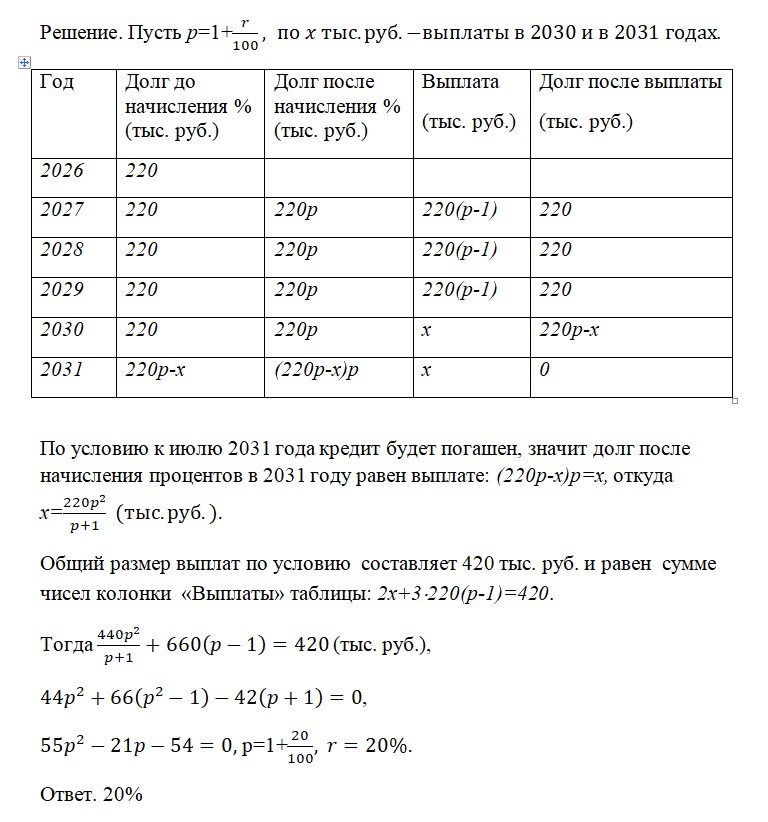
Пример 2.(Задание 15 вариант 22 из книги Математика. Подготовка к ЕГЭ-2023. Профильный уровень. 40 тренировочных вариантов по демоверсии 2023 года. Издательство «Легион»)

Решение:

Пример 3.(Задание 15 вариант 22 из книги Математика. Подготовка к ЕГЭ-2023. Профильный уровень. 40 тренировочных вариантов по демоверсии 2023 года. Издательство «Легион»)

Решение:

Похожие статьи
- Как решать задание 10 в ЕГЭ по математике (профиль)
- Как решать задание 9 в ЕГЭ по математике (профиль)
- Как решать задание 13 в ЕГЭ по математике (профиль)
- Как решать задание 18 в ЕГЭ по математике (профиль)




